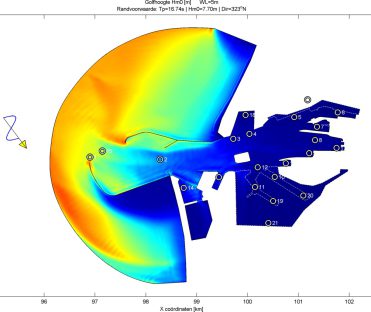
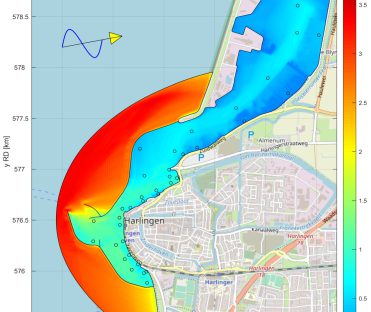
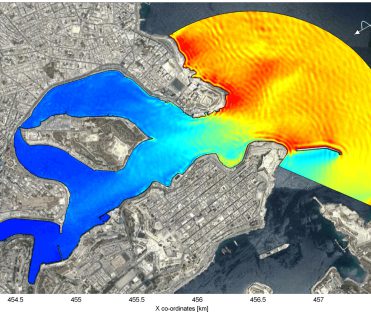
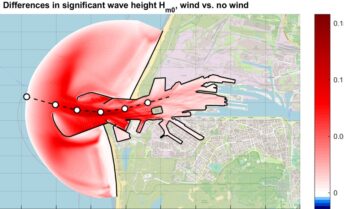
HARES (“HArbour RESonance”) is a two-dimensional numerical model for determining short wave propagation in near-shore domains, e.g. harbour basins. The model is based on the 2D Mild-Slope Equation and includes the physical phenomena of diffraction, refraction, shoaling, (partial) reflection, (partial) transmission, non-linear bottom friction, non-linear wave breaking, directional spreading and frequency spreading. HARES has been developed in-house by Svašek Hydraulics and is one of the fastest and most widely applicable Mild-Slope wave models currently available.

HARES is based on the Finite Element approach and applies a flexible mesh of linear triangles. This approach offers almost unlimited flexibility in grid generation. Special features, like complicated harbour and breakwater layouts, can be accurately incorporated into the grid. HARES is highly parallelised for efficient calculations on our in-house computational HPC cluster. HARES offers a large computational speed and can be applied interactively in port design processes.

HARES can deal with (partially) reflecting structures in a harbour and breakwaters that combine partial transmission and reflection properties. Given the structure characteristics, HARES automatically calculates the reflection and transmission coefficients based on the local incoming wave conditions.

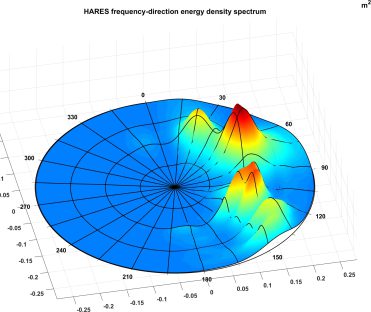
The model has a fast and efficient spectral treatment of bottom friction and wave breaking based on the entire wave spectrum, inspired by the spectral wave-energy model SWAN. HARES also offers the post-processing tool WAVEDIRECT, which enables the user to detect and analyse all local wave propagation directions within the HARES solution. In this way, it is also possible to construct detailed local 2D wave energy spectra.

HARES has been extensively validated against analytical solutions and laboratory conditions. See for example Eikema et al., 2018 which shows that HARES delivers accurate results compared to other software such as SWASH and SWAN.

HARES is approved by the Dutch Ministry of Infrastructure and Water Management (Rijkswaterstaat) to determine hydraulic boundary conditions inside harbours. These conditions can be used to assess the safety of the sea defences.

If you would like to discuss technical details or receive more specific information about the application and capabilities of HARES, we would be happy to speak with you personally. Please feel free to contact us for further information.